1977 Canadian MO Problems/Problem 2: Difference between revisions
No edit summary |
No edit summary |
||
| Line 7: | Line 7: | ||
== See Also == | == See Also == | ||
* [[1977 Canadian MO Problems]] | |||
* [[1977 Canadian MO]] | |||
[[Category:Olympiad Geometry Problems]] | |||
Revision as of 21:18, 25 July 2006
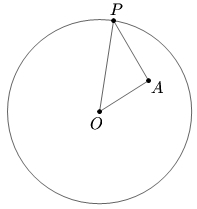
Let ![]() be the center of a circle and
be the center of a circle and ![]() be a fixed interior point of the circle different from
be a fixed interior point of the circle different from ![]() Determine all points
Determine all points ![]() on the circumference of the circle such that the angle
on the circumference of the circle such that the angle ![]() is a maximum.
is a maximum.