2012 AMC 10B Problems/Problem 14: Difference between revisions
format the equations |
No edit summary |
||
| Line 4: | Line 4: | ||
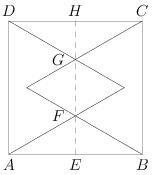
Observe that the rhombus is made up of two congruent equilateral triangles with side length equal to GF. Since AE has length <math>\sqrt{3}</math> and triangle AEF is a 30-60-90 triangle, it follows that EF has length 1. By symmetry, HG also has length 1. Thus GF has length <math>2\sqrt{3} - 2</math>. The formula for the area of an equilateral triangle of length s is <math>\frac{\sqrt{3}}{4}s^2</math>. It follows that the area of the rhombus is: | Observe that the rhombus is made up of two congruent equilateral triangles with side length equal to GF. Since AE has length <math>\sqrt{3}</math> and triangle AEF is a 30-60-90 triangle, it follows that EF has length 1. By symmetry, HG also has length 1. Thus GF has length <math>2\sqrt{3} - 2</math>. The formula for the area of an equilateral triangle of length s is <math>\frac{\sqrt{3}}{4}s^2</math>. It follows that the area of the rhombus is: | ||
<math>2 | <math>2\times\frac{\sqrt{3}}{4}(2\sqrt{3}-2)^2 = 8\sqrt{3} - 12</math> | ||
Thus, answer choice D is correct. | Thus, answer choice D is correct. | ||
Revision as of 20:10, 15 February 2013
Solution
Observe that the rhombus is made up of two congruent equilateral triangles with side length equal to GF. Since AE has length 
and triangle AEF is a 30-60-90 triangle, it follows that EF has length 1. By symmetry, HG also has length 1. Thus GF has length 
. The formula for the area of an equilateral triangle of length s is 
. It follows that the area of the rhombus is:
Thus, answer choice D is correct.
