1997 PMWC Problems/Problem I11: Difference between revisions
No edit summary |
Archimedes1 (talk | contribs) |
||
| Line 5: | Line 5: | ||
==Solution== | ==Solution== | ||
Let l and w be the length, and width, respectively, of one of the | Let <math>l</math> and <math>w</math> be the length, and width, respectively, of one of the small rectangles. | ||
<math>3w=2l</math> | <math>3w=2l</math> | ||
| Line 11: | Line 11: | ||
<math>l=\dfrac{3}{2}w</math> | <math>l=\dfrac{3}{2}w</math> | ||
<math>6750=\dfrac{15}{2}w^2</math> | <math>6750= 5lw = \dfrac{15}{2}w^2</math> | ||
<math>w=30</math> | <math>w=30</math> | ||
Revision as of 20:32, 26 April 2008
Problem
A rectangle ABCD is made up of five small congruent rectangles as shown in the given figure. Find the perimeter, in cm, of ABCD if its area is 
.
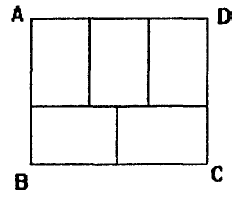
Solution
Let 
and 
be the length, and width, respectively, of one of the small rectangles.
The perimeter of the big rectangle is
See also
| 1997 PMWC (Problems) | ||
| Preceded by Problem I10 |
Followed by Problem I12 | |
| I: 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 T: 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 | ||
