2023 AMC 12B Problems/Problem 17: Difference between revisions

Revision as of 22:35, 15 November 2023

Problem

Triangle ABC has side lengths in arithmetic progression, and the smallest side has length $6.$ If the triangle has an angle of $120^\circ,$ what is the area of $ABC$ ?

$\textbf{(A) }12\sqrt{3}\qquad\textbf{(B) }8\sqrt{6}\qquad\textbf{(C) }14\sqrt{2}\qquad\textbf{(D) }20\sqrt{2}\qquad\textbf{(E) }15\sqrt{3}$

Solution 1

The length of the side opposite to the angle with $120^\circ$ is longest. We denote its value as $x$ .

Because three side lengths form an arithmetic sequence, the middle-valued side length is $\frac{x + 6}{2}$ .

Following from the law of cosines, we have $\begin{align*} 6^2 + \left( \frac{x + 6}{2} \right)^2 - 2 \cdot 6 \cdot \frac{x + 6}{2} \cdot \cos 120^\circ = x^2 . \end{align*}$

By solving this equation, we get $x = 14$ . Thus, $\frac{x + 6}{2} = 10$ .

Therefore, the area of the triangle is $\begin{align*} \frac{1}{2} 6 \cdot 10 \cdot \sin 120^\circ = \boxed{\textbf{(E) } 15 \sqrt{3}} . \end{align*}$

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Solution 2 (Analytic Geometry)

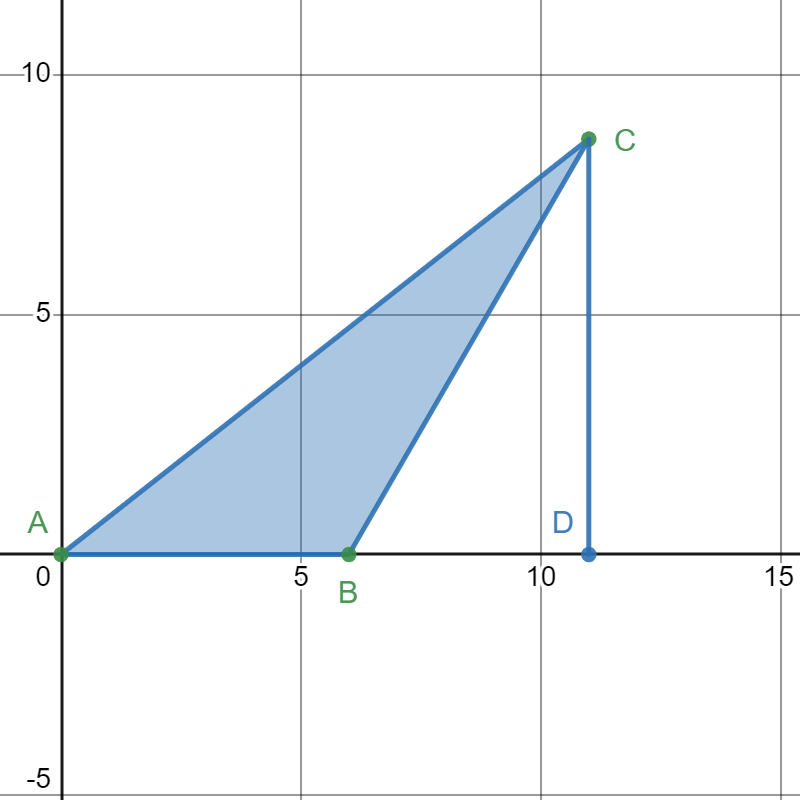
Since the triangle's longest side must correspond to the $120^\circ$ angle, the triangle is unique. By analytic geometry, we construct the following plot.

We know the coordinates of point $A$ being the origin and $B$ being $(6,0)$ . Constructing the line which point $C$ can lay on, here since $\angle B=120^\circ$ , $C$ is on the line $y=\sqrt{3}\left(x-6\right).$

I denote $D$ as the perpendicular line from $C$ to $AB$ , and assume $CD=k$ . Here we know $\triangle BCD$ is a $30^\circ-60^\circ-90-^\circ$ triangle. Hence $DC=\sqrt{3}k$ and $BC=2k$ .

Furthermore, due to the arithmetic progression, we know $AC=4k-6$ . Hence, in $\triangle ACD$ , $\left(4k-6\right)^{2}=\left(6+k\right)^{2}+3k^{2},$ $k=5.$

Thus, the area is equal to $\frac{1}{2}\cdot 6\cdot \sqrt{3} k=\boxed{\textbf{(E) } 15 \sqrt{3}}$ .

~Prof. Joker

Solution 3

Let the side lengths be $6$ , $6+d$ , and $6+2d$ . As $6+2d$ is the longest side, the angle opposite to it will be $120^{\circ}$ .

By the law of Cosine $(6+2d)^2 = 6^2 + (6+d)^2 - 2 \cdot 6 \cdot (6+d) \cdot \cos 120^{\circ}$ $4d^2 + 24d + 36 = 36 + 36 + 12 d + d^2 + 36 + 6d$ $3d^2 + 6d - 72 = 0$ $d^2 + 2d - 24 = 0$ $(d+6)(d-4)=0$

As $d>0$ , $d = 4$ , $6+d = 10$

Therefore, $[ABC] = \frac{ 6 \cdot 10 \cdot \sin 120^{\circ} }{2} = \boxed{\textbf{(E) } 15 \sqrt{3}}$

~isabelchen

@@ Line 47: / Line 47: @@
 Thus, the area is equal to <math>\frac{1}{2}\cdot 6\cdot \sqrt{3} k=\boxed{\textbf{(E) } 15 \sqrt{3}}</math>.
-- Prof. Joker
+~Prof. Joker
 ==Solution 3==

2023 AMC 12B (Problems • Answer Key • Resources)
Preceded by Problem 16	Followed by Problem 18
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search