Asymptote: Useful commands and their Output

Asymptote (Vector Graphics Language)

Getting Started - Basics - Drawing - Labeling - Filling - Useful functions - Examples - Macros and Packages Help - Reference - Advanced Asymptote - 3D Graphics - CSE5 Package - How to

For each of the following, we have put a blue dot at the origin in order to indicate relative location of the output on the coordinate plane. In other words, assume that before each of the examples below is the command

dot((0,0),blue);

In addition, a comment after a line such as //math - extension indicates that the command (in this case extension) used in that line is defined in the math package, thus motivating the import math; (or other appropriate package) line at the top of the example.

---

Example 1:

dot((20,0));

Output 1:

---

Example 2:

draw((0,0)--(50,0),BeginArrow);
draw((0,-10)--(50,-10),MidArrow);
draw((0,-30)--(50,-30),Arrows);

Output 2:

---

Example 3:

draw((0,0)--(50,0));
arrow((30,0),dir(180),green);

Output 3:

---

Example 4:

import math;
pair A,B,C,D,E;
A=(0,0); C=(50,0); B=(10,10); D=(40,20);
E=extension(A,B,C,D);  // math - extension
// extension(A,B,C,D) returns the intersection of lines AB and CD
draw(A--B); draw(C--D);
draw(B--E--D,orange);

Output 4:

---

Example 5:

import graph;
draw(Circle((0,0),20)); // graph - Circle

Output 5:

---

Example 6:

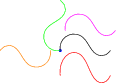
path p=(0,0)..(20,15)..(40,-5)..(50,0);
draw(p);
draw(rotate(90)*p,green);
draw(rotate(180,(-5,0))*p,orange);
draw(shift((5,20))*p,magenta);
draw(shift((0,-25))*yscale(1.4)*p,red);

Output 6:

---

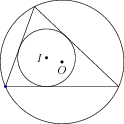
Example 7:

import olympiad;
unitsize(50);
pair A,B,C,O,I;
A=origin; B=2*right; C=1.5*dir(70);
O=circumcenter(A,B,C); // olympiad - circumcenter
I=incenter(A,B,C); // olympiad - incenter
draw(A--B--C--cycle);
dot(O);
dot(I);
draw(circumcircle(A,B,C)); // olympiad - circumcircle
draw(incircle(A,B,C)); // olympiad - incircle
label("",I,W);
label("",O,S);

Output 7:

---

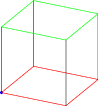
Example 8:

import three;
unitsize(1inch);
currentprojection=orthographic(1/2,-1,1/2); // three - currentprojection, orthographic
draw((0,0,0)--(1,0,0)--(1,1,0)--(0,1,0)--cycle3,red); //three - cycle3
draw((0,0,0)--(0,0,1));
draw((0,1,0)--(0,1,1));
draw((1,1,0)--(1,1,1));
draw((1,0,0)--(1,0,1));
draw((0,0,1)--(1,0,1)--(1,1,1)--(0,1,1)--cycle3,green);

Output 8:

See Also

Many more Asymptote examples