2006 AMC 12A Problems/Problem 13: Difference between revisions
Put official diagram. |
m moved image below problem statement |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
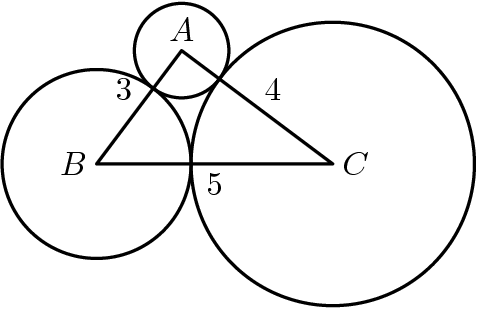
The [[vertex|vertices]] of a <math>3-4-5</math> [[right triangle]] are the centers of three mutually externally tangent [[circle]]s, as shown. What is the sum of the areas of the three circles? | |||
[[Image:Original_2006_12A_13.png]] | [[Image:Original_2006_12A_13.png]] | ||
<math> \mathrm{(A) \ } 12\pi\qquad \mathrm{(B) \ } \frac{25\pi}{2}\qquad \mathrm{(C) \ } 13\pi\qquad \mathrm{(D) \ } \frac{27\pi}{2}\qquad\mathrm{(E) \ } 14\pi</math> | <math> \mathrm{(A) \ } 12\pi\qquad \mathrm{(B) \ } \frac{25\pi}{2}\qquad \mathrm{(C) \ } 13\pi\qquad \mathrm{(D) \ } \frac{27\pi}{2}\qquad\mathrm{(E) \ } 14\pi</math> | ||
==Solution== | == Solution == | ||
Let the radius of the smallest circle be <math>r_A</math>, the radius of the second largest circle be <math>r_B</math>, and the radius of the largest circle be <math>r_C</math>. | Let the radius of the smallest circle be <math>r_A</math>, the radius of the second largest circle be <math>r_B</math>, and the radius of the largest circle be <math>r_C</math>. | ||
<cmath>r_A + r_B = 3</cmath> | <cmath>r_A + r_B = 3</cmath> | ||
Latest revision as of 12:57, 19 January 2021
Problem
The vertices of a 
right triangle are the centers of three mutually externally tangent circles, as shown. What is the sum of the areas of the three circles?
Solution
Let the radius of the smallest circle be 
, the radius of the second largest circle be 
, and the radius of the largest circle be 
.
![\[r_A + r_B = 3\]](http://latex.artofproblemsolving.com/d/3/2/d32fc5e73b196d772754dd22491fcd35a84bb5f3.png)
![\[r_A + r_C = 4\]](http://latex.artofproblemsolving.com/1/9/c/19c0750788a3a435260e2fd673e16c9ac408bd4f.png)
![\[r_ B + r_C = 5\]](http://latex.artofproblemsolving.com/5/b/0/5b0ea74a9c0df59da5cb769e4a8d0415e3c427ea.png)
Adding up all these equations and then dividing both sides by 2, we get,
![\[r_A + r_B + r_C = 6\]](http://latex.artofproblemsolving.com/7/d/1/7d1cefc3fb4362fcd5dbae413e070ba9c5bc3a71.png)
Then, we get 
, 
, and 
Then we get 
See also
| 2006 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 12 |
Followed by Problem 14 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. Error creating thumbnail: File missing
