Convex polygon: Difference between revisions
No edit summary |
|||
| Line 14: | Line 14: | ||
* [[Concave polygon]] | * [[Concave polygon]] | ||
* [[Convex polyhedron]] | * [[Convex polyhedron]] | ||
{{stub}} | {{stub}} | ||
[[Category:Definition]] | [[Category:Definition]] | ||
Revision as of 09:11, 23 September 2007
| This is an AoPSWiki Word of the Week for Sep 20-26 |
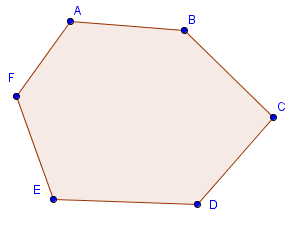
A convex polygon is a polygon whose interior forms a convex set. That is, if any 2 points on the perimeter of the polygon are connected by a line segment, no point on that segment will be outside the polygon.
All internal angles of a convex polygon are less than 
. These internal angles sum to 
degrees.
The convex hull of a set of points also turns out to be the convex polygon with some or all of the points as its vertices.
The area of a regular n-gon of side length s is 
See also
This article is a stub. Help us out by expanding it.
