Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2007 AMC 10B Problems/Problem 21: Difference between revisions

← Older edit
Rlz (talk | contribs)
5 edits
Added solution using ratios
Michaellin16 (talk | contribs)
editor
22 edits
 
(11 intermediate revisions by 8 users not shown)
Line 9: Line 9:
[[Image:2007AMC10B21.png|center]]
[[Image:2007AMC10B21.png|center]]


There are many similar triangles in the diagram, but we will only use <math>\triangle WBZ \sim \triangle ABC.</math> If <math>h</math> is the altitude from <math>B</math> to <math>AC</math> and <math>s</math> is the sidelength of the square, then <math>h-s</math> is the altitude from <math>B</math> to <math>WZ.</math> By similar triangles,
There are lots of similar triangles in the diagram, but we will only use <math>\triangle WBZ \sim \triangle ABC.</math> If <math>h</math> is the altitude from <math>B</math> to <math>AC</math> and <math>s</math> is the sidelength of the square, then <math>h-s</math> is the altitude from <math>B</math> to <math>WZ.</math> By similar triangles,
<cmath>\begin{align*}
<cmath>\begin{align*}
\frac{h-s}{s}&=\frac{h}{5}\\
\frac{h-s}{h}&=\frac{s}{5}\\
5(h-s)&=hs\\
5h-5s&=hs\\
5h-5s&=hs\\
5h&=s(h+5)\\
5h&=s(h+5)\\
Line 34: Line 35:
<cmath>\frac{ZB}{l} = \frac{4}{5} \rightarrow ZB = \frac{4}{5}l</cmath>
<cmath>\frac{ZB}{l} = \frac{4}{5} \rightarrow ZB = \frac{4}{5}l</cmath>


But then <math>\frac{5}{3}l+\frac{4}{5}l = CZ+ZB = CB = 4 \longrightarrow \frac{37}{15}l=4 \longrightarrow l = \frac{60}{37} \Longrightarrow \mathrm{(C)}</math>
But then <math>\frac{5}{3}l+\frac{4}{5}l = CZ+ZB = CB = 4 \longrightarrow \frac{37}{15}l=4 \longrightarrow l = \frac{60}{37} \Longrightarrow \boxed{\mathrm{(B)}\frac{60}{37}}</math>


==Solution 3(quick and ez)==
After drawing the figure, realize that triangle AXY is similar to ABC, so then, we know that if we call line segment XW 4d, AW must be 5d, so BW=3-5d and since line segment WZ is still 4d since WXYZ is a square, so since triangle WBZ is still similar to triangle ABC, (3-5d)/(4d) must equal 3/5, so solving, we get d=15/37 and that the value of 4d, or what we are looking for, is 60/37, or the answer B.
-Michaellin16
== Video Solution by OmegaLearn==
https://youtu.be/FDgcLW4frg8?t=4662
~ pi_is_3.14


==See Also==
==See Also==

Latest revision as of 21:32, 2 November 2025

Problem

Right $\triangle ABC$ has $AB=3, BC=4,$ and $AC=5.$ Square $XYZW$ is inscribed in $\triangle ABC$ with $X$ and $Y$ on $\overline{AC}, W$ on $\overline{AB},$ and $Z$ on $\overline{BC}.$ What is the side length of the square?

$\textbf{(A) } \frac{3}{2} \qquad\textbf{(B) } \frac{60}{37} \qquad\textbf{(C) } \frac{12}{7} \qquad\textbf{(D) } \frac{23}{13} \qquad\textbf{(E)} 2$

Solution 1

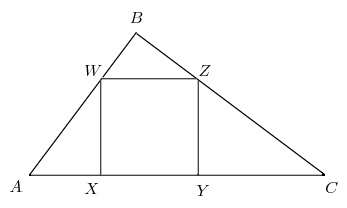
There are lots of similar triangles in the diagram, but we will only use $\triangle WBZ \sim \triangle ABC.$ If $h$ is the altitude from $B$ to $AC$ and $s$ is the sidelength of the square, then $h-s$ is the altitude from $B$ to $WZ.$ By similar triangles, \begin{align*} \frac{h-s}{h}&=\frac{s}{5}\\ 5(h-s)&=hs\\ 5h-5s&=hs\\ 5h&=s(h+5)\\ s&=\frac{5h}{h+5} \end{align*}

Find the length of the altitude of $\triangle ABC.$ Since it is a right triangle, the area of $\triangle ABC$ is $\frac{1}{2}(3)(4) = 6.$

The area can also be expressed as $\frac{1}{2}(5)(h),$ so $\frac{5}{2}h=6 \longrightarrow h=2.4.$

Substitute back into $s.$

\[s=\frac{5h}{h+5} = \frac{12}{7.4} = \boxed{\mathrm{(B) \ } \frac{60}{37}}\]

Solution 2

Let $l$ be the side length of the inscribed square. Note that $\triangle ZYC \sim \triangle WBZ \sim \triangle ABC$.

Then we can setup the following ratios:

\[\frac{CZ}{l} = \frac{5}{3} \rightarrow CZ = \frac{5}{3}l\] \[\frac{ZB}{l} = \frac{4}{5} \rightarrow ZB = \frac{4}{5}l\]

But then $\frac{5}{3}l+\frac{4}{5}l = CZ+ZB = CB = 4 \longrightarrow \frac{37}{15}l=4 \longrightarrow l = \frac{60}{37} \Longrightarrow \boxed{\mathrm{(B)}\frac{60}{37}}$

Solution 3(quick and ez)

After drawing the figure, realize that triangle AXY is similar to ABC, so then, we know that if we call line segment XW 4d, AW must be 5d, so BW=3-5d and since line segment WZ is still 4d since WXYZ is a square, so since triangle WBZ is still similar to triangle ABC, (3-5d)/(4d) must equal 3/5, so solving, we get d=15/37 and that the value of 4d, or what we are looking for, is 60/37, or the answer B.

-Michaellin16

Video Solution by OmegaLearn

https://youtu.be/FDgcLW4frg8?t=4662

~ pi_is_3.14

See Also

2007 AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 20 		Followed by
Problem 22
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. Error creating thumbnail: File missing

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2007_AMC_10B_Problems/Problem_21&oldid=264821"