2023 AMC 12B Problems/Problem 9: Difference between revisions

← Older edit

Latest revision as of 23:41, 24 June 2025

The following problem is from both the 2023 AMC 10B #13 and 2023 AMC 12B #9, so both problems redirect to this page.

Problem

What is the area of the region in the coordinate plane defined by

$| | x | - 1 | + | | y | - 1 | \le 1$ ?

$\text{(A)}\ 2 \qquad \text{(B)}\ 8 \qquad \text{(C)}\ 4 \qquad \text{(D)}\ 15 \qquad \text{(E)}\ 12$

Diagram

~diagram by grogg007

Solution 1

First consider, $|x-1|+|y-1| \le 1.$ We can see that it is a square with a side length of $\sqrt{2}$ (diagonal $2$ ). The area of the square is $\sqrt{2}^2 = 2.$

Next, we insert an absolute value sign into the equation and get $|x-1|+||y|-1| \le 1.$ This will double the square reflecting over x-axis.

So now we have $2$ squares.

Finally, we add one more absolute value and obtain $||x|-1|+||y|-1| \le 1.$ This will double the squares as we reflect the $2$ squares we already have over the y-axis.

Concluding, we have $4$ congruent squares. Thus, the total area is $4\cdot2 =$ $\boxed{\text{(B) 8}}$

~Technodoggo ~Minor formatting change: e_is_2.71828, mathkiddus ~Grammar and clarity: NSAoPS j

Solution 2 (Graphing)

We first consider the lattice points that satisfy $||x|-1| = 0$ and $||y|-1| = 1$ . The lattice points satisfying these equations are $(1,0), (1,2), (1,-2), (-1,0), (-1,2),$ and $(-1,-2).$ By symmetry, we also have points $(0,1), (2,1), (-2,1), (0,-1), (2,-1),$ and $(-2,-1)$ when $||x|-1| = 1$ and $||y|-1| = 0$ . Graphing and connecting these points, we form 5 squares. However, we can see that any point within the square in the middle does not satisfy the given inequality (take $(0,0)$ , for instance). As noted in the above solution, each square has a diagonal $2$ for an area of $\frac{2^2}{2} = 2$ , so the total area is $4\cdot2 =$ $\boxed{\text{(B) 8}}.$

~ Brian__Liu

Note

This problem is very similar to a past AIME problem (1997 P13)

https://artofproblemsolving.com/wiki/index.php/1997_AIME_Problems/Problem_13

~ CherryBerry

Solution 3 (Logic)

The value of $|x|$ and $|y|$ can be a maximum of 1 when the other is 0. Therefore the value of $x$ and $y$ range from -2 to 2. This forms a diamond shape which has area $4 \times \frac{2^2}{2}$ which is $\boxed{\text{(B) 8}}.$

~ darrenn.cp ~ DarkPheonix

Solution 4

We start by considering the graph of $|x|+|y|\leq 1$ . To get from this graph to $||x|-1|+||y|-1| \leq 1$ we have to translate it by $\pm 1$ on the $x$ axis and $\pm 1$ on the $y$ axis.

Graphing $|x|+|y|\leq 1$ we get a square with side length of $\sqrt{2}$ , so the area of one of these squares is just $2$ .

We have to multiply by $4$ since there are $4$ combinations of shifting the $x$ and $y$ axis.

So we have $2\times 4$ which is $\boxed{\text{(B) 8}}$ .

~ESAOPS

Solution 5 (Desperate)

There are $2$ sets of $2$ absolute value bars. Each of those $2$ absolute value bars can take on $2$ values, so we have $2 \cdot 2 \cdot 2 = 8$ cases. We guess that the answer is divisible by $8$ . The only answer choice that is divisible by $8$ is $\boxed{\text{(B)}~8}$ .

~ cxsmi

Video Solution 1 by OmegaLearn

https://youtu.be/300Ek9E-RrA

Video Solution 2 by MegaMath

https://www.youtube.com/watch?v=300yLhj4BI0&t=1s

Video Solution

https://youtu.be/Tic8qo-iQq4

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

@@ Line 9: / Line 9: @@
 <math>\text{(A)}\ 2 \qquad \text{(B)}\ 8 \qquad \text{(C)}\ 4 \qquad \text{(D)}\ 15 \qquad \text{(E)}\ 12</math>
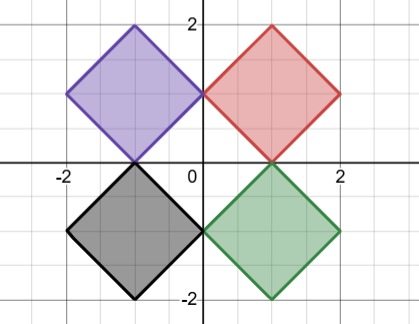
-==Solution==
+==Diagram==
+[[File:2023-AMC10B-13.png]]
+~diagram by [https://artofproblemsolving.com/wiki/index.php/User:grogg007 grogg007]
+==Solution 1==
 First consider, <math>|x-1|+|y-1| \le 1.</math>
-We can see that it's a square with radius 1 (diagonal 2). The area of the square is <math>\sqrt{2}^2 = 2.</math>
+We can see that it is a square with a side length of <math>\sqrt{2}</math> (diagonal <math>2</math>). The area of the square is <math>\sqrt{2}^2 = 2.</math>
+Next, we insert an absolute value sign into the equation and get <math>|x-1|+||y|-1| \le 1.</math> This will double the square reflecting over x-axis.
+So now we have <math>2</math> squares.
+Finally, we add one more absolute value and obtain <math>||x|-1|+||y|-1| \le 1.</math> This will double the squares as we reflect the <math>2</math> squares we already have over the y-axis.
+Concluding, we have <math>4</math> congruent squares. Thus, the total area is <math>4\cdot2 = </math> <math>\boxed{\text{(B) 8}}</math>
+~Technodoggo ~Minor formatting change: e_is_2.71828, mathkiddus ~Grammar and clarity: NSAoPS
+j
+==Solution 2 (Graphing)==
+We first consider the lattice points that satisfy <math>||x|-1| = 0</math> and <math>||y|-1| = 1</math>. The lattice points satisfying these equations
+are <math>(1,0), (1,2), (1,-2), (-1,0), (-1,2),</math> and <math>(-1,-2).</math> By symmetry, we also have points <math>(0,1), (2,1), (-2,1), (0,-1),
+(2,-1),</math> and  <math>(-2,-1)</math>  when  <math>||x|-1| = 1</math> and <math>||y|-1| = 0</math>.  Graphing and connecting these points, we form 5 squares. However,
+we can see that any point within the square in the middle does not satisfy the given inequality (take <math>(0,0)</math>, for instance). As
+noted in the above solution, each square has a diagonal <math>2</math> for an area of <math>\frac{2^2}{2} = 2</math>, so the total area is <math>4\cdot2 =</math>
+<math>\boxed{\text{(B) 8}}.</math>
+~ Brian__Liu
+==Note==
+This problem is very similar to a past AIME problem (1997 P13)
+https://artofproblemsolving.com/wiki/index.php/1997_AIME_Problems/Problem_13
+~ CherryBerry
+==Solution 3 (Logic)==
+The value of <math>|x|</math> and <math>|y|</math> can be a maximum of 1 when the other is 0. Therefore the value of <math>x</math> and <math>y</math> range from -2 to 2. This forms a diamond shape which has area <math>4 \times \frac{2^2}{2}</math> which is <math>\boxed{\text{(B) 8}}.</math>
+~ darrenn.cp
+~ DarkPheonix
+==Solution 4==
+We start by considering the graph of <math>|x|+|y|\leq 1</math>. To get from this graph to <math>||x|-1|+||y|-1| \leq 1</math> we have to translate it by <math>\pm 1</math> on the <math>x</math> axis and <math>\pm 1</math> on the <math>y</math> axis.
+Graphing <math>|x|+|y|\leq 1</math> we get a square with side length of <math>\sqrt{2}</math>, so the area of one of these squares is just <math>2</math>.
+We have to multiply by <math>4</math> since there are <math>4</math> combinations of shifting the <math>x</math> and <math>y</math> axis.
+So we have <math>2\times 4</math> which is <math>\boxed{\text{(B) 8}}</math>.
+~ESAOPS
+==Solution 5 (Desperate)==
+There are <math>2</math> sets of <math>2</math> absolute value bars. Each of those <math>2</math> absolute value bars can take on <math>2</math> values, so we have <math>2 \cdot 2 \cdot 2 = 8</math> cases. We guess that the answer is divisible by <math>8</math>. The only answer choice that is divisible by <math>8</math> is <math>\boxed{\text{(B)}~8}</math>.
+~ cxsmi
+==Video Solution 1 by OmegaLearn==
+https://youtu.be/300Ek9E-RrA
-Next, we add one more absolute value and get <math>|x-1|+||y|-1| \le 1.</math> This will double the square reflecting over x-axis.
+==Video Solution 2 by MegaMath==
-So now we got 2 squares.
+https://www.youtube.com/watch?v=300yLhj4BI0&t=1s
-Finally, we add one more absolute value and get <math>||x|-1|+||y|-1| \le 1.</math> This will double the squares reflecting over y-axis.
+==Video Solution==
-In the end, we got 4 squares.  The total area is <math>4\cdot2 = </math> <math>\boxed{\text{(B)} 8}</math>
+https://youtu.be/Tic8qo-iQq4
-~Technodoggo ~Minor formatting change: e_is_2.71828
+~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
 ==See Also==

2023 AMC 10B (Problems • Answer Key • Resources)
Preceded by Problem 12	Followed by Problem 14
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

2023 AMC 12B (Problems • Answer Key • Resources)
Preceded by Problem 8	Followed by Problem 10
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search